Standard Deviation Importance Score Calculator
Importance Score Analysis
Importance Rankings (Top Contributors)
Critical Values
Low Impact Values
Score Distribution
Interpretation & Recommendations
The standard deviation importance calculator is a conceptual tool that ranks SD zones in a normal distribution by their “importance” in shaping the data’s story. It blends factors like data density, spread behavior, variance contribution, and z-score patterns to assign scores, highlighting which zones—such as 0–1 SD or beyond 2 SD—matter most.
This isn’t about probability (like empirical rule percentages) or confidence intervals; it’s a ranked interpretation of structural roles. For learners, it clarifies why central zones dominate; for analysts, it aids prioritizing insights. For more detailed variance insights, see our Standard Deviation Percentage Contribution Calculator and Variance Distribution Analyzer.
What Is SD “Importance” and Why Does It Matter?
SD “importance” is a conceptual score reflecting how much an SD zone influences a normal distribution’s key traits—like where data clusters or how spread occurs. It’s not a strict math term but a blend: high density zones score high for informativeness, while sparse tails rank low despite extremes.
In a bell curve, not all regions are equal—the 0–1 SD zone often tops rankings as it’s dense and variance-rich. Understanding this helps interpret data: central zones reveal typical behavior, outer ones highlight rarities.
Why it matters: Guides focus in analysis, like ignoring low-importance tails for core insights. It demystifies distribution structure for beginners.
How the Standard Deviation Importance Score Calculator Works
The standard deviation importance calculator evaluates SD zones conceptually, ranking them by blended metrics for a holistic view.
Density Score: Measures curve height—central zones score high for clustering.
Variance Score: Assesses spread contribution—balances density with squared distance.
Spread Score: Factors z-score magnitude—farther zones note extremity but lower density.
Combined Importance Score: Weights elements (e.g., density 40%, variance 30%, spread 20%, z-score 10%) for an aggregate.
Final Rank: Outputs like:
Zone 1 (0–1 SD): Most Important (high density, major variance).
Zone 2 (1–2 SD): Moderately Important (balanced insights).
Zone 3 (>2 SD): Low Importance (rare, less informative).
This ranks SD zones, emphasizing density vs spread in z-score importance tool style.
Example: Importance Ranking of SD Zones
Let’s apply the calculator to a normal distribution (μ=0, σ=1):
| SD Zone | Importance Score | Interpretation |
|---|---|---|
| 0–1 SD | Highest | Most dense & informative—core data story. |
| 1–2 SD | Moderate | Useful for mid-range variability. |
| >2 SD | Low | Rare extremes, low overall impact. |
For test scores (μ=75, σ=10), 0–1 SD (65–85) ranks highest—most scores here drive patterns. This shows SD contribution analysis in action.
Density, Variance & Spread — How They Influence Importance
Density, variance, and spread interplay to define zone importance.
Density: Curve height—peaks at mean, boosting central importance for data clustering.
Variance Contribution: Squared deviations—central adds via volume, outer via distance.
Spread (Z-Score Distance): Measures extremity—outer zones highlight outliers but rank lower due to rarity.
Together, they create rankings: high-density centers dominate.
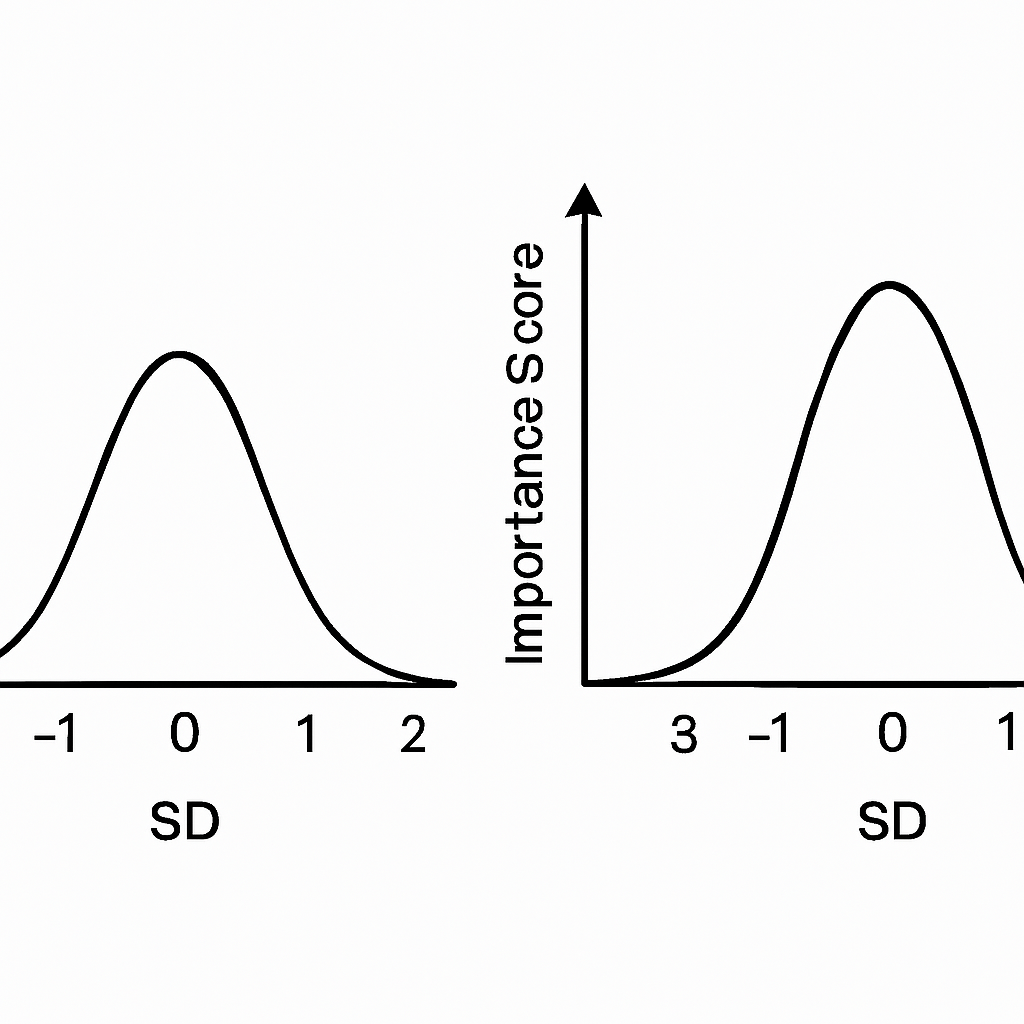
Why Importance ≠ Probability
Importance scoring differs from probability, which counts likelihood. Probability says ~68% within 1 SD—focusing frequency. Importance weighs structural roles: density for clustering, variance for spread impact.
A zone with low probability (beyond 2 SD) might have moderate importance if it pulls variance. This avoids equating rarity with irrelevance.
Even though probability beyond 2 SD is small, its importance is not zero — extreme values influence variance and shape interpretation.
Real-World Scenarios Where SD Importance Helps
In test scores, 0–1 SD ranks most important—average performances here reveal grading patterns, guiding educators.
For product quality in manufacturing, central zones (high importance) show consistent outputs; low-importance tails flag rare defects without overemphasis.
In biological measurements like heart rates, mid-range zones (moderate importance) highlight typical variations, aiding health analysis.
These scenarios show distribution importance zones, with central high for core insights, outer low for exceptions.
Limitations
This tool assumes theoretical normal distributions—real data may skew rankings. It doesn’t analyze datasets or compute probabilities.
Importance is conceptual, not statistical test—use for learning, not decisions. Z-score behavior assumes symmetry; non-normal data invalidates.
For non-ideal cases, check normality first.
FAQs
Related Tools
To dive into density, try our Standard Deviation Density Contribution Tool. For variance breakdowns, explore the Variance Distribution Analyzer. See SD contributions in Understanding Percentage Contribution of Standard Deviations in a Distribution. Rank extremes with the Empirical Rule Extreme Value Finder. Start with basics at our Empirical Rule Calculator.
Conclusion
The standard deviation importance calculator ranks SD zones by density, spread, variance, and z-scores, revealing which matter most in normal distributions. Central zones often rank highest for informativeness, while tails are low-importance rarities.
This deepens grasp of distribution structure, with density driving core importance. Encourage exploring related tools for practical applications.
Empirical Rule Custom Zone Calculator
Empirical Rule Custom Zone Calculator Create and calculate custom zones like -3σ to -1σ in normal distributions using the Empirical Rule. Approximate probabilities for segmented bell curve analysis.
Try CalculatorEmpirical Rule Outlier Detector
Quickly identify mild and extreme outliers using ±2σ and ±3σ thresholds in normal distributions, with Z-scores and bell curve visuals for clear analysis.
Try CalculatorOutlier Threshold Calculator (Mean ± k·SD Tool)
Customize outlier boundaries with any k-value for flexible detection, ideal for analysts adjusting sensitivity in datasets like exam scores or quality checks.
Try CalculatorNormality Check Before Outlier Detection Tool
Assess if your data fits a normal distribution via skewness, kurtosis, and histograms—essential before applying empirical rule methods to avoid errors.
Try Calculator