Understanding Range Probability in Empirical Rule With Examples

Range probability refers to the likelihood that a value falls between two specific points in a dataset. This article focuses on how the Empirical Rule (68–95–99.7 Rule) helps estimate these probabilities in a normal distribution, emphasizing middle-range coverage and between-value chances. We’ll explore the basics, examples, and manual calculations to make empirical rule range probability clear for beginners. Whether you’re a student or analyst, you’ll see why this approximation is useful for quick insights. For hands-on calculations, try our main statistics calculator .

What Is Range Probability in a Normal Distribution?

In a normal distribution—a bell-shaped curve where data clusters around the mean—range probability is the chance a value lies between two numbers. It’s the area under the curve between two points, representing the proportion of data in that interval.

For example, the probability of a score between 70 and 90 on a test is the range probability. This differs from tail probability (extremes) or percentiles (rankings). In normal distributions, range probabilities are symmetric around the mean, making them predictable.

Bell curve with mean 100 and SD 15, shaded between 85 and 115 labeled “Range Probability Example: ~68% between 85 and 115”.

How the Empirical Rule Estimates Range Probability

The Empirical Rule provides a quick way to estimate range probability in normal distributions:

  • 68% of data falls within ±1 standard deviation (SD) of the mean.

  • 95% within ±2 SD.

  • 99.7% within ±3 SD.

For ranges matching these, the probability is direct (e.g., ±1 SD = 68%). For partial ranges, estimate by dividing zones (e.g., from mean to +1 SD = ~34%). This empirical rule probability method is approximate but useful for symmetric intervals.

Example: A range from -1 SD to +1 SD has a probability of ~68%. From -2 SD to 0 (half of ±2 SD) is ~47.5%.

Range Probability Examples (With Visuals)

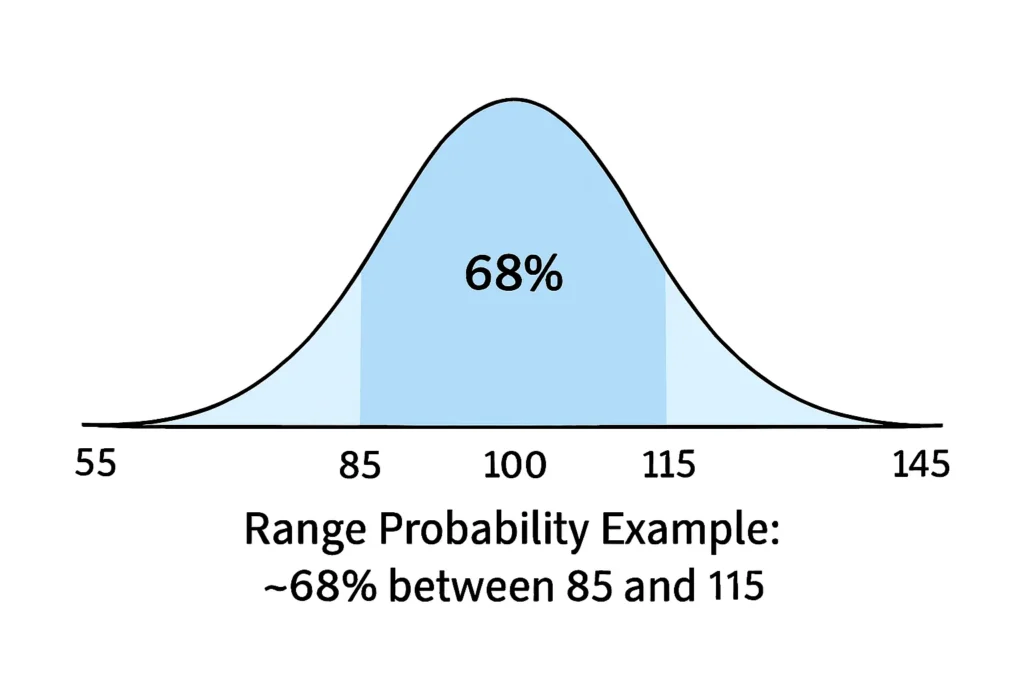
Example 1: Symmetric Full Range (±1 SD)

Mean = 100, SD = 15
Range = 85 to 115 (±1 SD)
Probability ≈ 68% (full 1 SD zone).
This is the probability between two values matching the rule.

Normal distribution bell curve (mean 100, SD 15) with shaded area between 85 and 115, labeled “68% probability between 85 and 115”.

Example 2: Partial Range Within ±2 SD

Mean = 50, SD = 10
Range = 50 to 70 (0 to +2 SD)
Probability ≈ 47.5% (half of 95%).
This shows interval coverage vs exact probability estimation.

Example 3: Asymmetric Range

Mean = 120, SD = 20
Range = 100 to 140 (-1 SD to +1 SD)
Probability ≈ 68%.
For non-symmetric, adjust by calculating SD distances.

Why the Empirical Rule Is an Approximation (Not Exact)

The Empirical Rule is a handy estimate but approximate. It works best for perfectly normal distributions; real data may be slightly skewed. For exact probabilities, use z-scores or tables — the rule’s 68-95-99.7% are rounded values.

Difference between empirical rule and z-score: Z-scores give precise probabilities for any range; the rule is for quick SD multiples. For non-normal data, it’s less accurate.

How to Calculate Range Probability Manually Using the Empirical Rule

  1. Find SD Distances: Compute z-scores for each value: ( z = \frac{x – \mu}{\sigma} ).

  2. Align with Zones: Check if the range matches ±1, ±2, or ±3 SD (e.g., ±1 SD = 68%).

  3. Estimate for Partial Ranges: Divide zones (e.g., from mean to +1 SD = 34%).

  4. Adjust for Asymmetry: Add/subtract zone portions (e.g., from -0.5 SD to +1 SD ≈ 53.2%).

Micro-Example: Mean = 100, SD = 15, range = 100 to 115 (+1 SD) → ~34%. For custom calculations, use our custom zone tool.

Real-World Use Cases of Range Probability

  • Education: Probability a student scores between 70 and 90 on a test (e.g., ~68% if ±1 SD).

  • Psychology: Chance an IQ is between 85 and 115 (±1 SD = 68%).

  • Business: Probability a product’s weight is between two specs (±2 SD = 95%).

  • Health: Likelihood a patient’s blood pressure is in a normal range (±1 SD = 68%).

These empirical rule probability example scenarios show everyday applications.

Range Probability vs Tail Probability vs Percentiles

  • Range Probability: Likelihood between two points (e.g., 68% within ±1 SD).

  • Tail Probability: Likelihood in extremes (e.g., < -2 SD = 2.5%).

  • Percentiles: Ranking (e.g., 84th percentile = z = 1).

For tail calculations, try our tail probability tool .

Related Tools

FAQs

It’s the likelihood data falls between two values, estimated by the rule’s zones (e.g., 68% between ±1 SD).

 

It’s accurate for normal distributions but approximate; exact values need z-tables.

 

Yes, if the range aligns with SD multiples; otherwise, z-scores help adjust.

 

The actual values are approximately 68.27%, 95.45%, 99.73% — rounded for simplicity in teaching.

 

Don’t use it for skewed, non-normal, or small datasets, as the percentages won’t be accurate.

 

For non-symmetric ranges or precise probabilities, especially in research.

 

Conclusion

Understanding range probability in the Empirical Rule unlocks quick insights into normal distributions, from symmetric intervals to partial ranges. With examples like test scores or IQs, you’ve seen how this approximate method simplifies probability between two values. Whether for class or analysis, the rule’s 68-95-99.7 zones make data intuitive. To instantly compute the probability between two values, try our Empirical Rule Range Probability Calculator, or explore our Empirical Rule Middle % Probability Calculator, Empirical Rule Symmetric Interval Calculator, and Empirical Rule Custom Zone Calculator.

Other Tools

Z-Score to Graph Plotter

Plot Z-scores on a bell curve and see where your value lies. Understand percentiles and probabilities at a glance.

Try Calculator

Empirical Rule Percentile Calculator

Quickly estimate percentiles in a normal distribution using the 68-95-99.7 rule. Input mean, standard deviation, and a score to find its percentile rank.

Try Calculator

Percentile Rank Calculator

Find your score’s percentile rank without needing mean or standard deviation. Input your score and rank to see where you stand in any dataset.

Try Calculator

Normal Distribution to Percentile Visualizer

Visualize your score on a bell curve with shaded percentile areas. Enter mean, standard deviation, and a score to see its rank in a normal distribution.

Try Calculator